Ohjelmointi ylioppilaskirjoituksissa

Ensimmäinen huomioitava asia on se, että ohjelmointia ei lopulta tule olemaan lukiossa kovin paljon. Pitkässä matematiikassa on yhteensä 26 opintopistettä, jotka on jaettu 12 moduuliin. Ohjelmointi on yhdessä 2 opintopisteen moduulissa yhdessä lukuteorian kanssa. Ohjelmoinnin painoarvo LOPS:eissa ei
siis ole suuri.

Toinen huomioitava seikka on se, että kyseessä on matematiikan oppiaine. Matematiikan ylioppilaskokeiden pääasia on jatkossakin matematiikka. Ohjelmoinnissakin tärkeintä on matemaattinen osuus eli algoritminen ajattelu. Tätä algoritmista ajattelua voi ilmentää monella eri tavalla. Kevään 2021 tehtävässä 8 ohjelmakoodin saattoi toteuttaa esimerkiksi pseudokoodina, taulukkolaskentaohjelmalla tai ihan konkreettisena ohjelmakoodina. Pseudokoodi ei tietenkään ole hyvä vaihtoehto silloin, jos koodi pitää pystyä oikeasti ajamaan, eikä pelkkä rakenteen pohtiminen riitä. Toteutustavasta riippumatta tärkeintä on kuitenkin matemaattinen ajatus.

Tavoitteet

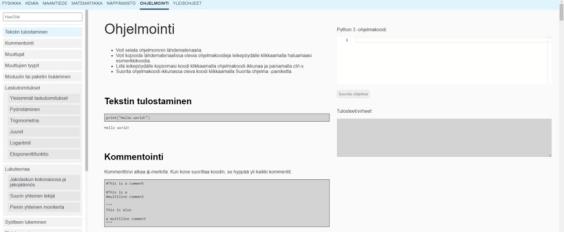
Abitin toteutuksessa ohjelmointikielenä on Python. Tämän lisäksi voi ohjelmoida ja ajaa selaimella JavaScriptiä. Opiskelijoiden ohjelmointitaidot voivat kuitenkin olla peräisin eri ohjelmointikielien harjoittelusta. Lisäksi tarkan syntaksin muistaminen ei aina ole helppoa tai edes tarkoituksenmukaista: tavoitteet ovat matematiikassa ja algoritmisessa ajattelussa ja näiden algoritmien toteuttamisessa, ei tarkan syntaksin ja puolipisteiden tai kaksoispisteiden muistamisessa. Abitissa onkin esittely tyypillisistä kommennoista ja tarpeellisista kirjastoista.

Toteutus

Lukiossa ohjelmointikursseja pitävien opettajien haastattelujen perusteella ohjelmointia opetetaan lähitulevaisuudessa pitkän matematiikan vanhan opetussuunnitelman MAA12-kurssilla, uuden opetussuunnitelman valtakunnallisessa MAA11-moduulissa ja mahdollisilla lukiokohtaisilla valinnaisilla, nimenomaan ohjelmointiin keskittyvillä kursseilla. Edellisessä tärkeintä on ympäristön nopea käyttöönotto ja yksinkertaisuus, jälkimmäisessä käytetään ammattimaisia ohjelmistonkehitysympäristöjä (integrated development environment, IDE).

Tällä hetkellä Abitissa voi ohjelmoida Pythonilla GIMP-kuvankäsittelyohjelmassa, Texas Instrumentsin Nspire -laskinohjelmassa, Javascriptillä selaimessa sekä pienellä kikkailulla tikulla mukana olevilla Python-, Perl- ja sh/bash-skriptikielillä. Aiempaa helppokäyttöisemmän ohjelmointiympäristön suunnittelun lähtökohdaksi otettiin MAA11 ja sille soveltuva enintään muutamien kymmenien rivien ohjelmointiin soveltuva ympäristö. Varsinaisen muokkaus- ja ajoympäristön lisäksi koeympäristöön haluttiin tuoda käsikirjahenkinen materiaali.

Ohjelmointiympäristö päätettiin sijoittaa osaksi koeympäristön ohjeita, koska se näkyy koeympäristön ulkopuolella osoitteessa https://cheat.abitti.fi. Koeympäristön ohjeet ovat avointa lähdekoodia, joten siihen on helppo ehdottaa parannuksia tai sijoittaa identtinen ohjelmointimahdollisuus osaksi jotain muuta oppimisympäristöä.

Abitin ohjelmointiympäristössä kokelas voi kopioida esimerkkikoodin ohjeista, muokata sitä ja suorittaa koodin. Ohjelmakoodin ja tulosteen voi kopioida vastaukseen tekstinä tai kuvankaappauksena. Abitti-tikulla olevien skriptikielien (esim. Perl, bash) käyttöä ei ole tarkoitus jatkossakaan tukea.

Esimerkki vanhasta ylioppilaskoetehtävästä

Kevään 2020 tehtävänä 12 oli seuraava todennäköisyyslaskennan tehtävä:

Kahden positiivisen luvun a ja b geometrinen keskiarvo on √(ab).
1. Anna esimerkki välin 2–100 kahdesta eri kokonaisluvusta a ja b, joille √(ab) on kokonaisluku. (3 p.)
2. Satunnaislukugeneraattori arpoo toisistaan riippumatta kaksi kokonaislukua
väliltä 1–100 niin, että jokaisen luvun todennäköisyys on 1/100 . Mikä on todennäköisyys sille, että arvottujen lukujen geometrinen keskiarvo on kokonaisluku? Voit laskea tapahtuman klassisen todennäköisyyden tarkasti tai esittää sille simulointiin perustuvan arvion. (9 p.)

Tässä tehtävässä ensimmäinen kohta vaati vain esimerkin löytämisen. Toinen kohta oli ratkaistavissa esimerkiksi taulukkolaskentaohjelmalla. Simuloinnin voisi toteuttaa Pythonilla esimerkiksi näin:

import random
import math
k=0
2
i=0
while i<500:
  a=random.randint(1,100)
  b=random.randint(1,100)
  c=math.sqrt(a*b)
  i=i+1
  print(a,b,c)
  if (c-round(c,0)==0):
    k=k+1
print(k/500)

Ratkaisun idea on se, että arvotaan lukupareja a ja b annetulta väliltä ja tarkistetaan antaako tämä arvottu lukupari geometriseksi keskiarvoksi kokonaisluvun vai ei. Lasketaan, miten monen lukuparin kohdalla tämä toteutuu ja jaetaan kokonaisotoksen koolla.

Tämä olisi simulointiratkaisu. Käytännössä tässä ratkaisussa huomaa, että jos koodin ajaa muutaman kerran läpi, vaihtelee tulos melko paljon, mutta arvion saa näin tehtyä. Kaikkien tapausten läpikäynti puolestaan onnistuisi seuraavasti:

import math
k=0
i=1
while i<101:
  j=1
  while j<101:
    c=math.sqrt(i*j)
    j=j+1
    if (c-round(c,0)==0):
      k=k+1
  i=i+1
print(k/10000)

Lopuksi jaetaan suotuisien tapausten määrä kaikkien mahdollisten tapausten määrällä.

Koeympäristön ohjeen kehitysversio on saatavilla osoitteessa https://cheat.test.abitti.fi. 

Palautetta ohjelmointiympäristöstä voi lähettää osoitteeseen abitti@ylioppilastutkinto.fi.